
It's wise to be sceptical of some types of computational analysis
August 2018
Analysis is only as good as the model and the model is only as good as its worst assumption.
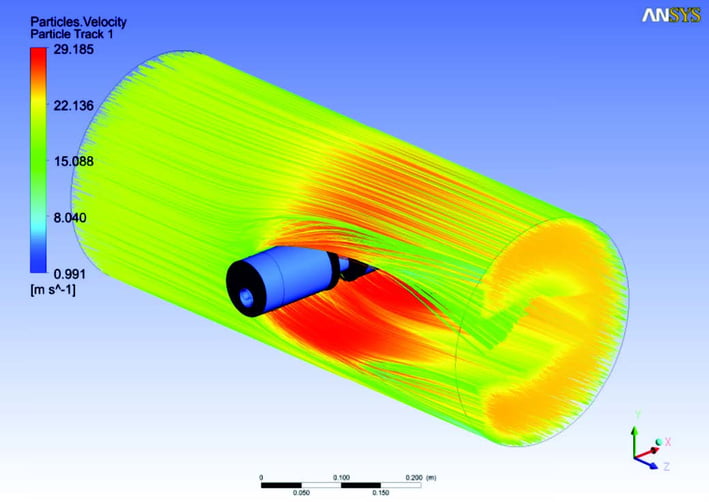
Nevertheless, modern finite element (FE) tools do provide better than ever support for accurate analysis with intelligently assisted generation of meshes, iterative closed loop mesh refinement in key areas and tight integration with CAD systems to speed the design iteration process.
This applies equally to thermal modelling, stress analysis, computational fluid dynamics (CFD) or even magnetic field modelling.

Modern finite element based analytical tools serve a key role in engineering
Used appropriately, FE analysis can prove invaluable in many scenarios, such as when:
- actual testing is too slow or too expensive (for example when the gas flowing through the manifold being optimised is at several hundred degrees or the test-pieces would require expensive tooling to produce, or if the equipment required to run a real world test doesn’t exist yet)
- direct parameter measurement is difficult or impossible, on the real equipment, whereas modelling enables the determination of alternative, more measurable surrogate parameters which correlate with the quantities of interest
- it is necessary to determine the sensitivity of performance to small changes in key dimensions of a design, so that appropriate manufacturing tolerances can be determined
- a variety of visualisations need to be used to understand where a design is under-performing, so that improvement, effort can be focused in the most cost effective areas
In many cases, exact answers are not essential (comparative answers are the primary goal) but with CFD, for example, a well validated model may be expected to produce figures that fall well within 5% of the figures measured in the real world.

Key things that can help to get better results
- find some way to correlate analysis with a more measurable configuration at the earliest opportunity. For example, pick a slower, colder, or lower pressure test point, but with comparable Reynold’s number to the target scenario. See how theory and practice align
- determine the bounds of the inaccuracies caused by the assumptions you have knowingly made. Be realistic about how close your answers can ever be
- streamline the iterative process. The faster you can try something new, the more iterations you’ll fit in, and the better the final answer
- use all the visualisation tools at your disposal, and learn to see what is actually going on. The analysis tools should illuminate the problem, not spit answers out of a black box
- even with modern computing power, complex analyses can still take several hours. Plan carefully to learn the most from each cycle
Key skills with any such tools are:
- knowing when (and when not) to use them
- understanding how to use them to increase your knowledge rather than replace it
If you need any advice regarding this article, then please email answers@42t.com.
Share this article:
Related Articles

News, Connectedness
Early prototypes help companies to succeed - by 42T's David Griffin in Eureka! magazine

Connectedness
New Electronics prints 42T’s article on how to get around the supply chain squeeze

News, Connectedness, Industrial
42T experts speak at Engineering Design Show (EDS)

What will you ask us today?
We believe in asking the right questions to drive innovation; when we know the right questions, we generate the ideas to answer them.

